Day4 監督式學習可視化

前言

昨天有提到了蠻多基本的概念，如果還沒有看的可以先去前一天稍微對監督式學習有點概念喔。

實作介紹

今天我會用程式來將幾個常見的算法變的可視化，首先是迴歸，我們以簡單線性迴歸來示範。

簡單線性迴歸

程式碼及說明

1. 引入必要的庫

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

首先，我們引入了 numpy、pandas 和 matplotlib 這些基本的數據處理和繪圖庫，並從 sklearn.linear_model 模組中引入了 LinearRegression 模型。

2. 生成示範數據

np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

這段程式碼生成了一些隨機的示範數據。np.random.seed(0) 設置隨機數生成器的種子，以確保每次運行程式時生成的隨機數據相同。X 是自變數，取值範圍在 0 到 2 之間，y 是依變數，它是 X 的線性函數（帶有一些噪音）。

3. 創建線性迴歸模型並進行訓練

model = LinearRegression()
model.fit(X, y)

我們創建了一個線性迴歸模型實例 model，並用生成的數據 X 和 y 進行訓練。

4. 進行預測

X_new = np.array([[0], [2]])
y_predict = model.predict(X_new)

我們定義了一個新的自變數範圍 X_new，並使用訓練好的模型進行預測，得到相應的預測值 y_predict。

5. 繪製結果

plt.scatter(X, y, color='blue', label='Actual data')
plt.plot(X_new, y_predict, color='red', label='Fit line')
plt.title('Simple Regression Analysis')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()

生成的圖片顯示了簡單線性迴歸的結果，是不是還是不懂那是甚麼呢?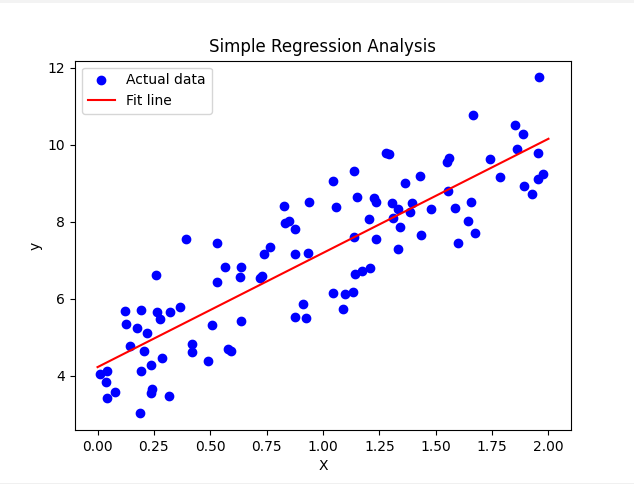

圖片說明

• 散點圖 (藍色點)：
  • 每個藍色點代表一個實際的數據樣本，顯示自變數𝑋與目標變數𝑦之間的關係。這些點可能因為噪音而散布在某個趨勢周圍。
• 擬合線 (紅色線)：
  • 紅色線是線性迴歸模型擬合的結果，表示模型預測的趨勢。這條線是通過最小化預測值與實際值之間的誤差所得到的。
• 圖片的意義
  • 趨勢顯示：紅色擬合線表明當𝑋增加時，𝑦的值也隨之增加，顯示出一種正向的線性關係。
  • 模型擬合的效果：通過觀察藍色點與紅色線的接近程度，可以評估模型的擬合效果。如果大部分點都靠近紅色線，則表示模型擬合得很好。

如果以實例來說明的話

• 藍色的點：每個藍色點代表一個實際的房子數據，顯示不同房子面積（平方公尺）與其實際售價（萬元）的關係。例如：

  • 面積 50 平方公尺，售價 100 萬元
  • 面積 80 平方公尺，售價 160 萬元
  • 面積 120 平方公尺，售價 250 萬元
    這些點會因為市場波動和其他因素而散布在圖上，形成一些不規則的分佈。
    藍色點的意義：反映了實際市場數據中的各個房子的面積和售價。這些數據可能會因為不同的房子條件（如位置、裝修等）而有所不同。

• 紅色的線：紅色線則表示模型擬合的房價預測趨勢，這條線代表當房子的面積增加時，預測的售價也會隨之增加。它可能是這樣的一個線性關係：

  • 當面積增加每增加 10 平方公尺，預測售價增加大約 20 萬元。
    紅色線的作用：提供了一個簡單的預測模型，讓我們能夠對未來未觀測到的房子進行價格預測。比如，如果一個新房子的面積為 70 平方公尺，根據紅色線可以預測其售價約為 140 萬元。

KNN近鄰演算法

程式碼及說明

1. 引入必要的庫

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier

首先，我們一樣引入了 numpy 和 matplotlib 這些基本的數據處理和繪圖庫，並從 sklearn.datasets 引入了 make_classification 用於生成分類數據，從 sklearn.model_selection 引入了 train_test_split 用於數據集的切分，從 sklearn.neighbors 引入了 KNeighborsClassifier 來建立 K 近鄰分類器。

2. 生成隨機分類數據

X, y = make_classification(n_samples=100, n_features=2, n_informative=2,
                             n_redundant=0, n_clusters_per_class=1, random_state=0)

這段程式碼生成了一些隨機的二維分類數據。X 是特徵矩陣，包含 100 個樣本，每個樣本有兩個特徵。y 是目標標籤。

3. 切分數據集

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

我們將數據集切分為訓練集和測試集，其中 70% 用於訓練，30% 用於測試。

4. 創建 KNN 模型並進行訓練

knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)

我們創建了一個 K 近鄰分類器，設置鄰居數為 3，並用訓練數據進行訓練。

5. 創建網格以可視化決策邊界

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
                     np.arange(y_min, y_max, 0.01))

創建一個網格來可視化決策邊界。xx 和 yy 是網格點的坐標。

6. 預測決策邊界

Z = knn.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

用訓練好的模型對網格點進行預測，得到決策邊界。
7. 繪製結果

plt.figure(figsize=(10, 6))
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.coolwarm)  # Decision boundary
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, marker='o', label='Training data', edgecolor='k')
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, marker='s', label='Test data', edgecolor='k')
plt.title('K-Nearest Neighbors Classification Visualization')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()

繪製 K 近鄰分類結果。背景顏色顯示了不同的分類區域，訓練數據點用圓形標記，測試數據點用方形標記。標題設為 "K-Nearest Neighbors Classification Visualization"，X 軸和 Y 軸分別標記為 "Feature 1" 和 "Feature 2"。最後，顯示圖例並展示圖表。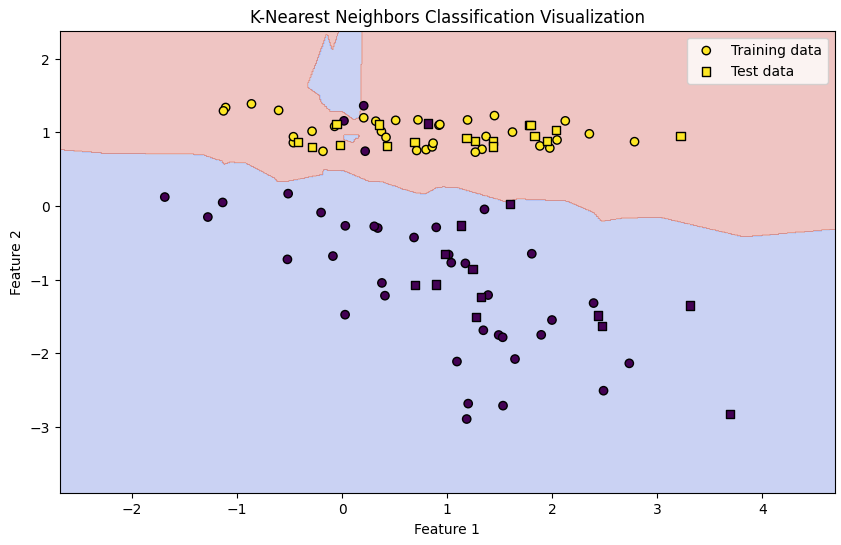

圖片組成

1. 決策邊界 (背景顏色)：

   • 圖片的背景顏色表示不同的預測類別區域。每種顏色代表一個類別，顯示了模型在特定區域內的分類決策。當輸入點位於某個顏色區域時，模型將其分類為該類別。

2. 訓練數據 (圓形標記)：

   • 圓形標記的點代表訓練集中的數據點，每個點顏色與其真實標籤一致。這些點用於訓練 K 近鄰模型，幫助模型學習決策邊界。

3. 測試數據 (方形標記)：

   • 方形標記的點代表測試集中的數據點，同樣顏色表示其真實標籤。這些點用來評估模型的預測效果。

圖片的意義

• 分類決策：決策邊界展示了模型是如何根據訓練數據生成的，並且這條邊界決定了每個區域的類別。例如，如果一個新數據點落在某個顏色區域內，模型將其分為該顏色所代表的類別。

• 模型的靈活性：K 近鄰算法根據距離來進行分類，因此決策邊界可能是曲線的，顯示出模型能夠適應數據的複雜性。

• 過擬合的風險：如果決策邊界過於複雜（如有很多小曲折），可能表明模型過擬合訓練數據，對於未見數據的泛化能力較差。

• 數據分佈的影響：訓練數據的分佈會影響決策邊界的形狀。若訓練數據在某個區域特別密集，則該區域的決策邊界可能會更加明確。